
David
García Colín
El origen dialéctico del código binario y la historia de la computación

En el mundo hay dos clases de personas: las que saben que el código binario tiene un trasfondo dialéctico y las que no. En 1720 fue publicado un artículo del Leibniz titulado “Explicación de la aritmética binaria que únicamente utiliza los caracteres 0 y 1, junto a algunas notas sobre su utilidad y sobre cómo ella le da sentido a las antiguas figuras Chinas de Fu Xi”. Por primera vez se expone en un sentido moderno y para fines de cómputo el código binario, que es el lenguaje de todos los procesadores actuales. En este notable artículo Leibniz expone su código binario en relación con el “I Ching”, el “Libro de los cambios” o “Libro de las mutaciones”; un texto sagrado chino con más de 3 mil años de antigüedad, que se basa en filosofía dialéctica del yin yang. Es uno de los libros más antiguos que la humanidad conserva. En este libro se encuentran un conjunto de “trigramas binarios” compuestos por una serie de barras continuas y discontinuas que representan al yin yang. La barra discontinua representa el yin (o principio femenino) y la barra continua al yang (principio masculino). Ambas simbolizan la unidad dialéctica de los opuestos, el cambio y la transformación de todas las fuerzas en el universo. Leibniz fue fundador de la filosofía clásica alemana de la cual Marx va a retomar el método dialéctico para utilizarlo como una herramienta de la transformación revolucionaria.
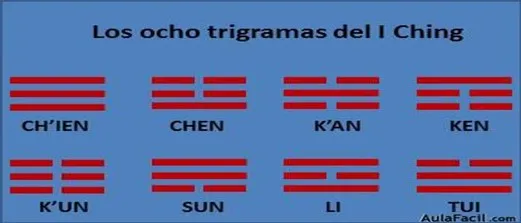
Los “trigramas” se componen de un conjunto de tres barras apiladas horizontalmente. Probablemente este conjunto se motivó en los tres niveles del universo (cielo, tierra e inframundo), que solían tener gran importancia en las culturas antiguas. Con las barras continuas y discontinuas son posibles 8 combinaciones de trigramas: son los trigramas básicos que representan fuerzas de la naturaleza. Pueden observarse algunos en la bandera de Corea del Sur. A su vez, estos 8 trigramas básicos pueden combinarse en 64 hexagramas (o conjunto de seis barras apiladas horizontalmente) diferentes. Mientras que los bytes modernos contienen una serie de 8 bits –unos y ceros– los hexagramas chinos contienen un conjunto de seis barras continuas o rotas. Estos conjuntos tenían fines adivinatorios y se leían como actualmente se leen las cartas o los horóscopos: de forma vaga u oracular para que cada persona le encuentre un sentido místico. Pero en uno de estos conjuntos Leibniz encontró un sentido matemático y científico que da origen al sistema binario moderno.

Veremos que el
ajedrez, el código binario y el desarrollo de la inteligencia artificial tiene
puntos de confluencia muy interesantes con los que nos habremos de topar más
adelante. Por ahora comentemos de pasada que el gran maestro de ajedrez Liu
Wenche sostiene que las 64 casillas del tablero de ajedrez estuvieron
inspiradas en el Libro de los cambios, afirma que el Chaturanga de la India fue
producto de un juego mucho más antiguo.
La
Ilustración y la necesidad de calcular con exactitud
Leibniz vivió
en la época de la ilustración, cuando la burguesía en ascenso rompía los viejos
dogmas de la iglesia y desafiaba las barreras sociales del feudalismo,
adentrándose en el conocimiento científico de la realidad que las nuevas
relaciones sociales en ascenso requerían. La medición y exactitud eran
exigencias de los nuevos descubrimientos mecánicos, ópticos, náuticos, balísticos,
etcétera; que preparaban el camino de la revolución industrial. Leibniz mismo
sugirió la máquina de vapor incluso antes de los inventores normalmente
conocidos (Papin, Savery, Newcomen o Watt).
No es casualidad, tampoco, que Leibniz y Newton descubrieran el cálculo
diferencial e integral casi al mismo tiempo o que el propio Leibniz construyera
una calculadora mecánica que podía sumar, restar, multiplicar y sacar raíces
cuadradas, superando a su predecesora “la máquina de Pascal” que sólo podía sumar
y restar. Unos treinta años antes que Leibniz el gran filósofo español Juan
Caramuel expuso el sistema binario también en relación con cálculos
matemáticos, aunque de una forma un tanto menos completa que Leibniz, lo que
muestra que el descubrimiento de Leibniz ya estaba en el ambiente. Éste
escribió: “Es indigno de hombres excelentes perder horas como esclavos en el
trabajo del cálculo, porque si se usaran máquinas, podría delegarse con
seguridad a cualquier persona”.
Notablemente
Leibniz diseñó una calculadora –además de la ya mencionada “máquina de
Leibniz”– que funcionaba con el principio del código binario, a través de una
serie de bolas de metal que caían en ranuras. Pero como muchas de sus
brillantes ideas nunca la llevó a la práctica, aunque seguramente con la
tecnología de su tiempo hubiera sido casi imposible realizarla.
Con una
motivación matemática similar, Leibniz adelantó los principios del cálculo
proposicional o “calculus ratiocinator”, como él lo llamaba; la idea de
calcular con proposiciones o juicios, a la manera como se calcula con números,
para determinar la validez del pensamiento y evitar discusiones estériles.
Engels escribió que Leibniz “dispersó brillantes ideas en su derredor, sin
preocuparse de si el mérito de ellas le era otorgado a él o a algún otro”[1].
El propio Leibniz decía que constantemente le surgían ideas desordenadas sobre
toda clase de temas que plasmaba en cartas y papeles sin ningún orden en
particular y que muchas veces se perdían incluso para él mismo.
Con el fin de
facilitar los cálculos Leibniz ideó el código binario. En lugar de usar los
diez números del sistema decimal, sólo se usarían unos y ceros. Si en el
sistema decimal existe una potencia de diez en la posición de las cifras (en el
número 111, por ejemplo, el 1 de la derecha vale la unidad, el que le sigue a
la izquierda representa la decena y el siguiente la centena), en el sistema
binario los números van elevados a la potencia de dos según su posición, en una
progresión exponencial de base dos: 1,2,4,8,16,32, etcétera. Así, el 10 en
sistema binario representa el 2, porque el uno va en el lugar del 2, el 4 se
escribe 100, el 5 se escribe 101, el 8: 1000 y así sucesivamente.
Este sistema, aunque poco práctico para escribir grandes números, es muy práctico para hacer cálculos. Pueden realzarse sumas, multiplicaciones y divisiones de forma muy sencilla. Si queremos, por ejemplo, multiplicar 8 por 2 solo tenemos que mover la unidad un lugar a la izquierda: si 8 se escribe 1000, 16 se escribe como 10,000. De esta forma, Leibniz explica que “al reducir los números a los más simples principios, como 0 y 1, aparece un orden maravilloso por todas partes”[2]. Descubrió que ordenando los números binarios en tablas se podían localizar con facilidad los números cuadrados, cúbicos, algunas potencias; los números triangulares, piramidales; todos los cuales aparecen periódicamente a intervalos regulares. Curiosamente la misma progresión exponencial la encontramos en la leyenda india de Sisa sobre el origen del ajedrez: Sisa solicitó al rey que, como recompensa por haber inventado el juego, le concediera un grano de trigo por la primer casilla, dos por la segunda, 4 por la tercera y así hasta completar las 64 casillas del tablero, resultando un número astronómicamente grande.

Dialéctica
de los unos y ceros
Al igual que el
taoísmo y el yin yang, que tienen un indudable mensaje dialéctico, la filosofía
de Leibniz, iniciadora de la filosofía clásica alemana, estaba empapada de un
contenido dialéctico. Podemos afirmar que la historia de la filosofía
dialéctica puede resumirse en los esfuerzos contradictorios y desiguales por
emanciparla de su contenido místico original. Hegel va a sistematizar a
conciencia, aunque de una forma idealista, el pensamiento dialéctico de sus
predecesores y Marx va a poner ese método, que estaba de cabeza, sobre una
firme base materialista. “Sabes mi admiración por Leibniz”, escribió Marx a
Engels[3]. Si Leibniz va a separar el sistema binario de la forma religiosa en
que se encontraba en el “Libro de los cambios”, Marx va a separar el método
dialéctico del sistema idealista característico de la filosofía clásica
alemana.
Aunque Leibniz
fue un pensador idealista y religioso –en parte atrapado en el pensamiento
metafísico y formalista–, su dialéctica tenía un contenido racional. En su
monadología expresaba una especie de atomismo espiritual o idealista, afirmaba
que de la mónada principal –o Dios– emanaba un orden racional que armonizaba a
todas las demás mónadas del universo. Las mónadas eran unidades cerradas en sí
mismas pero orientadas por la razón divina. Ya los atomistas de la antigüedad
habían afirmado que toda la realidad se componía de los átomos y el vacío y
Leibniz, de forma similar, sostenía que la unidad era representada por las
mónadas, en tanto el completo vacío y “la jungla sombría” pertenecían al cero.
El trasfondo dialéctico presente en el pensamiento de Leibniz era terreno
fértil para ideas como el código binario e incluso el propio cálculo
diferencial –que Leibniz ideó al mismo tiempo que Newton– que lleva implícita
la noción de infinito; tema al que, por cierto, Marx dedicó su atención,
dejando notas sobre la dialéctica del cálculo.
Engels en
“Dialéctica de la naturaleza” hizo interesantes reflexiones sobre las
implicaciones dialécticas de la unidad y el cero. “Si cada número contiene la
unidad, en la medida en que está compuesto por completo de unos sumados, la
unidad, asimismo, contiene todos los otros números”[4]. Y esta interesante
reflexión explica, en esencia, la función del uno en el sistema binario. Pero
el sistema binario sería imposible sin el cero, Engels anotó también:
“El cero no
carece de contenido porque sea la negación de una cantidad definida. Por el
contrario, posee un contenido muy definido (…) En verdad, el cero es más rico
en contenido que cualquier otro número. Colocado a la derecha de cualquier
otro, otorga a éste, en nuestro sistema de números, un valor décuple”[5].
En el sistema
binario el cero otorga al número a su izquierda un valor correspondiente a una
sucesión exponencial de base dos. Generalizando esto, tal como anotó Engels
retomando una cita de Hegel, “la nada de algo es una nada determinada”[6]. El
ser y la nada: el ser que se desenvuelve generando otras determinaciones, la
nada que determina al ser. Sin el uno el cero es nada, necesita la cantidad
para determinarse y cobrar contenido; pero la unidad sin el cero pierde
potencia, pierde a su eje de equilibrio que la une con su opuesto negativo y
con otros ejes en el plano cartesiano.
Todo esto está contenido e implícito en el código binario.
Leibniz entendió que en el I Ching había un mensaje matemático que se había perdido bajo el peso del misticismo religioso y que había escapado a todos los observadores de su tiempo. La ordenación canónica de los hexagramas de I Ching –conocida como “La secuencia del rey Wen” o “Secuencia recibida”– tiene una motivación adivinatoria y mística. Pero una ordenación alternativa, la ordenación de Shao Yong –compuesta por el año mil d.C. – no es otra cosa que la representación numérica del 0 al 64. Esto resulta claro si interpretamos la barra continua como uno y las discontinua como cero, leyendo la secuencia de arriba abajo y de izquierda a derecha. El primer hexagrama contiene sólo barras fragmentadas, o sea sólo ceros, representa el cero; la segunda tiene una barra continua en el nivel superior, o en el lugar de las unidades, vale uno; el siguiente tiene la barra continua en el segundo nivel, el del número dos, vale dos, y así sucesivamente hasta el número 64. Tenemos la representación numérica en código binario en una simbología con más de tres mil años de antigüedad.

El
código binario y las maneras de contar
A pesar de la
simplicidad del código binario, la mayoría de los sistemas de numeración son
decimales por la sencilla razón de que la humanidad aprendió a contar y
descubrió los números usando los dedos de las manos; lo que ya de por sí es una
confirmación asombrosa del pensamiento materialista que afirma que los números
surgieron de la observación de la realidad material y la práctica social de los
seres humanos.
Los mayas
usaban un sistema vigesimal porque también contaban con los dedos de los pies,
mientras que aun hoy existen tribus en África que tienen un sistema de base
cinco, pues sólo usan los dedos de una mano. Hay una pequeña comunidad en
Papua, Nueva Guinea, que tiene el sistema de numeración más simple que pueda
imaginarse, sólo tiene dos números. Aunque suele citarse como ejemplo del
código binario su sistema no es posicional y carece del conocimiento del número
cero, lo que hacen simplemente es sumar con sus dos números para decir la cifra
que desean. “Morots” es 1 y “Serok” dos. El 5 lo llaman “serok a serok a
morots” (2+2+1). Como no requieren contar grandes cantidades, pues su forma de
vida no permite la acumulación, este sistema es más que suficiente.
La tradición de
la antigua China atribuye a Fuxi la invención de los trigramas. Fuxi es
mencionado por Leibniz en su artículo. Es un personaje semimitológico que se
pierde en el origen mismo de la civilización China. Una leyenda confucionista
afirma: “En el principio no existían ni la moral ni el orden social. Los
hombres sólo conocían a sus madres, no a sus padres. Cuando estaban
hambrientos, buscaban comida; cuando estaban satisfechos, tiraban los restos.
Devoraban los animales con la piel y el pelo, bebían su sangre y se vestían con
pieles y juncos. Entonces llegó Fuxi y miró hacia arriba y contempló lo que
había en los cielos y miró hacia abajo y contempló lo que ocurría en la tierra.
Unió al hombre con la mujer, reguló los cinco cambios y estableció las leyes de
la humanidad. Concibió los ocho trigramas para conseguir el dominio sobre el
mundo”. Esta leyenda es muy interesante porque nos habla de forma nebulosa de
la condición social anterior al surgimiento de la civilización, cuando los
seres humanos eran cazadores recolectores e imperaba un sistema de filiación
centrado en la mujer: “los hombres sólo conocían a sus madres”. Pero con la
civilización y la propiedad privada nació la familia centrada en el varón y surgieron
las leyes del Estado y los trigramas como un sistema ideológico de una clase
social dominante.
Parece ser que
en ese periodo de transición los adivinos o chamanes usaban trozos de aquilea
rotas y continuas que representaban el yin yang y que apilaban en grupos de
tres para responder a preguntas que necesitaban una respuesta mágica. Si este
sistema de adivinación estaba vinculado a un sistema de numeración muy
primitivo es algo que sólo se puede especular. A juzgar por algunos
jeroglíficos de 4,400 años de antigüedad, los antiguos egipcios sí
desarrollaron un sistema binario para hacer cuentas, aunque al final se impuso
en la práctica el sistema decimal. También el sistema de numeración que se
consolidó con la civilización en China fue el decimal y si los trigramas se
usaron alguna vez para contar de ello quedó solamente su uso oracular y mágico.
La ordenación numérica de Sao Yong parece ser que fue una excepción a la regla.
El
código binario desde Leibniz hasta la Unión Soviética
Antes de
Leibniz y aparte de las filosofías de la antigüedad, habían existido
incursiones en el código binario. El matemático indio Pingala, en el siglo III
antes de Cristo, ideó un sistema binario a partir de su descubrimiento del
cero, cuyo objetivo era la medición de las sílabas largas y cortas en los
libros sagrados. En 1605, en un contexto de nacimiento de las relaciones
sociales burguesas, Francis Bacon sugirió el uso de un código binario para
encriptar mensajes políticos. El Leibniz español, Juan Caramuel, fue un gran filósofo
materialista y seguidor de las ideas de Descartes. No sólo desarrolló los
logaritmos, entre otros muchos estudios, sino que, treinta años antes que
Leibniz, como parte de su exploración de otros sistemas numéricos diferentes al
de base 10, propuso un sistema binario para resolver algunos problemas
matemáticos. Pero después de que Leibniz expusiera el código binario en un
sentido más moderno, éste tuvo que esperar, como una curiosidad excéntrica, más
de 250 años el “sueño de los justos” antes de encontrar plena aplicación y
revolucionar al mundo moderno.
El Sistema
Morse y el Código Braille, desarrollados en el siglo XIX, son también códigos
binarios y constituyen ejemplos de sus primeros usos prácticos, el primero
basado en sonidos largos y cortos y el segundo con una serie de puntos. Con el
inicio de la revolución industrial y la producción en serie, que encontró gran
parte de su aplicación en la industria textil, se usó por vez primera, en el
año 1801, las tarjetas perforadas para registrar patrones que el telar de
Jacquar plasmaba en sus tejidos. Al mismo tiempo se mejoraban las llamadas
“maquinas diferenciales” o calculadoras mecánicas, herederas de la “máquina de
Pascal”, en las que el mismo Leibniz había estado involucrado un siglo antes.
Ada Lovelace,
hija del famoso poeta inglés Lord Byron, fue asistente de Charles Babbage quien
trabajaba en una “máquina diferencial”. El intelecto de Lovelace fue producto
de una educación aristocrática muy esmerada y apasionada por las matemáticas y
la mecánica. Pero mientras Babbage estaba más interesado en las operaciones
aritméticas que podía realizar la máquina, Ada fue más allá e inspirada por las
instrucciones de las tarjetas perforadas del telar de Jacquar propuso que
podían usarse también para introducir instrucciones a la “máquina diferencial”
y programar a la máquina para realizar cualquier tarea.
Lovelace
escribió en una de sus notas: “Puede decirse que la primera (la computadora)
teje dibujos algebraicos, del mismo modo que el telar de Jacquard teje flores y
hojas». Esbozó lo que se considera el primer algoritmo de la historia, la
primera programación de una computadora a través de instrucciones en tarjetas
perforadas para que una computadora escribiera una serie de números. Sugirió la
existencia de un estado neutro en las tarjetas perforadas, lo que adelantaba el
uso del código binario en ellas. Con un
pensamiento audaz vaticinó que una máquina podría incluso componer música:
«Supongamos,
por ejemplo, que las relaciones fundamentales entre los sonidos, en el arte de
la armonía, fueran susceptibles de tales expresiones y adaptaciones: la máquina
podría componer piezas musicales todo lo largas y complejas que se quisiera».
Leibniz había
escrito más de cien años antes: “La música es el placer que experimenta la
mente humana al contar sin darse cuenta de que está contando”. Las notas de
Lovelace fueron publicadas en 1843 en una revista científica. Pero sus ideas no
fueron tomadas en serio por la comunidad científica y machista de su tiempo.
Lovelace se hizo adicta a las apuestas y perdió mucho dinero tratando de
encontrar una fórmula que predijera al ganador, enferma de cáncer y presionada
por su madre “dejó de ser materialista” y se volvió religiosa. Murió en 1852 y
fue enterrada junto a su padre.
Charles Babbage
fue uno de los personajes, junto a Napoleón y Benjamín Franklin, que se
enfrentó a un autómata, llamado El Turco, que jugaba ajedrez y en giras por
Europa y América derrotó a jugadores fuertes. Era una época en que se
construían exquisitos mecanismos de relojería y autómatas. El público estaba
fascinado por un mecanismo, que no sólo reproducía movimientos humanos, sino
parecía reproducir la inteligencia humana. Pero no era más que un truco de
magia sofisticado. Dentro de la mesa de El Turco, además del mecanismo de
relojería que era mostrado al público antes y después de la partida, se
escondían jugadores fuertes de baja estatura que, con un juego de espejos e
imanes, manipulaban el mecanismo de poleas y engranajes.
Dos años
después de la muerte de Lovelace, en 1854, el matemático inglés George Boole
simbolizó algunos argumentos lógicos en un código binario de 0 y 1, donde 1
significa verdadero y 0 falso. Se trata de una especie de circuitos lógicos que
utilizará el matemático estadounidense Claude Shannon para diseñar los primeros
circuitos digitales a finales de los años treinta del siglo XX.
La máquina
Colossus –que normalmente se considera como la primera computadora de la
historia, aunque años antes George Stibitz ya había diseñado una computadora
conocida como “modelo k”– fue construida para decodificar los mensajes
encriptados de los nazis, trabajaba con un código binario y tarjetas
perforadas. En un contexto de guerra parecido al que animó a Francis Bacon a
pensar en un código binario para encriptar mensajes, ese mismo método se
utilizó para desencriptar en el contexto de la Segunda Guerra Mundial. Pero para que Colossus realizara una tarea
diferente había que modificar físicamente su engranaje y cableado, es decir no
podía cambiarse su programación.
Era una máquina
enorme –de allí su nombre– y sorprende que hoy un pequeño dispositivo que cabe
en el bolsillo del pantalón tenga mucho más poder que Colossus. No existía la
noción de software separada del hardware, lo que constituye una prueba de que
incluso en programación primero vino el hardware (materia) antes del software
(programa). A partir de esta limitante al matemático inglés Alan Turing se le
ocurrió una idea, que en esencia ya había tenido Ada Lovelace muchas décadas
antes: diseñar una máquina que pudiera realizar cualquier tarea simplemente
cambiando su programación a través de algoritmos, proyecto que denominó
“máquina universal”.
Turing fue
procesado en 1952 por homosexual, castrado químicamente y orillado al suicidio
en 1954. Como una muy mala broma la reina de Inglaterra retiró los cargos
contra Turing –después de la movilización del movimiento de diversidad sexual–
¡Hasta el 2013! Por su parte Shannon falleció en 2001 con un Alzheimer muy
avanzado, ya sin poder recordar los aportes que hizo a la memoria de la
humanidad. Con ironía su esposa puso en su epitafio “A él le hubiera
fascinado”.
Como fruto de
la planificación económica, la Unión Soviética estuvo a la vanguardia en la
generación de computadoras para fines bélicos y de exploración espacial, cosa
que normalmente se oculta o se omite por los comentaristas burgueses. Esto es
más sorprendente si consideramos que la URSS emergió de un nivel económico muy
bajo, semifeudal, y tras sufrir una terrible guerra civil y los catastróficos efectos
de la invasión nazi.
Inicialmente la
burocracia estalinista desconfió de la cibernética al mismo tiempo que
declaraba la genética como un invento burgués, pero pronto descubrieron que
esta disciplina era muy útil para fines militares y para el control de redes
eléctricas. En los años veinte Serguéi A. Lébedev diseñó circuitos que podían
controlar los aumentos de potencia en las redes de energía, lo que terminó por
convencer incluso a los lerdos burócratas estalinistas de la utilidad de la
computación.
Lébedev fue el
patriarca de la computación soviética, estuvo involucrado en la producción de
quince ordenadores distintos, desde los que usaban válvulas hasta los circuitos
que usan los ordenadores modernos. Desarrolló el primer sistema computacional
antibalístico y para 1961 las computadoras soviéticas eran las más avanzadas
del mundo. Fueron las primeras en alcanzar el millón de operaciones por segundo
y en la misión espacial Apolo-Soyuz lograron el procesamiento de datos de la
misión media hora antes que la NASA, lo que mostró la superioridad de las
computadoras soviéticas. El proyecto espacial soviético era la envidia del
mundo. Tampoco debemos olvidar que el primer campeonato mundial de ajedrez de
computadoras fue ganado por el programa soviético Kaisa, en 1974.
Lébdev, además,
firmó la carta de los 300 en 1955, donde un grupo de científicos condenó al
farsante Lysenko, que se oponía a la teoría de la evolución de Darwin, quien
había sido protegido de Stalin. A principios de los setenta, con un criterio
estrecho y pragmático, la burocracia tomó la decisión de copiar a la IBM 360
para fines comerciales a lo que se opuso Lébedev poco antes de su muerte. La
decisión de la burocracia afectó negativamente el desarrollo tecnológico de la
Unión Soviética.
Positivismo
lógico y dialéctica en computación
La ideología
Hollywoodense atribuye la invención de los procesadores a Turing como si
hubieran surgido de su cabeza como Minerva de la cabeza de Zeus. Pero hemos
visto que la computadora de Turing no fue sino la cristalización de un proceso
anterior bastante largo y profundo cuyos conocimientos básicos lo preceden: el
código binario, la máquina diferencial, las tarjetas perforadas y los
algoritmos, los circuitos lógicos y electrónicos, etcétera.
De igual forma
los fundamentos de la computación suelen asociarse al formalismo lógico y
matemático, pues tanto Boole como Turing eran logicistas y el último estuvo
interesado en el proyecto de reducir las matemáticas a la lógica formal. Pero
sin menoscabo de los aportes de gente como Boole y Turing la interpretación
filosófica del sistema binario y la programación no es monopolio de la lógica
formal ni puede reducirse a ella. El proyecto logicista de reducir las
matemáticas al formalismo lógico resultó infundado como mostró Gödel. Fue un
camino errado que, sin embargo, rindió frutos al menos en el sentido de
demostrar que no se pueden eliminar las contradicciones en el seno de las
matemáticas.
Tampoco el
sistema binario y la computación pueden reducirse a la lógica formal. La información
en bits no es la simple oposición lógica entre verdadero y falso, entre unos y
ceros. Cada bit del lenguaje computacional no tiene sentido en sí mismo sino
sólo como unidad de información en forma de bytes –conjunto mínimo de
información– y los programas tampoco tienen sentido como bytes aislados sino
como una unidad de millones y millones de bytes que codifican un programa o un
software específico. Entre los simples dígitos de unos y ceros y lo que vemos
en el monitor de la computadora existen toda una serie de saltos cualitativos.
Pero un programa o conjunto de programas no flotan en el vacío, requieren de un
soporte material llamado hardware o soporte físico en forma de circuitos,
chips, el CPU, monitor, etcétera; mismos que surgieron del conocimiento del
universo material, fundamentalmente del control de los seres humanos sobre los
electrones. Y sin embargo, el hardware sería poco más que una inútil caja con
una pantalla sin un programa que lo haga funcionar. Entre ellos existe una
relación dialéctica similar al de materia y subjetividad; la segunda no existe
sin la primera.
A su vez el
hardware y el software interactúan en forma de una serie de dispositivos de
entrada y de salida: las señales del mouse o del teclado entran y son
procesadas para dar una respuesta de salida, ya sea en la pantalla o a través
de una impresora. Pero la información tecleada es, a su vez, una señal de
salida del cuerpo humano que se convierte en entrada para la computadora. Las
causas se convierten en efectos y los efectos en causas. La realidad puede
convertirse en virtual –como sucede en una videoconferencia– así como lo
virtual se convierte en real cuando, por ejemplo, una impresora en 3D
materializa un proyecto o se imprime un libro. Pero la mayoría de las veces la
materialidad que surge así es sólo formal, como la de una maqueta, que sólo
cobrará todo su contenido cuando se produce como un objeto terminado.
Todas estas
interacciones y saltos cualitativos se entienden mucho mejor desde una
perspectiva dialéctica y materialista. Más aún, hemos tratado de demostrar que,
en su origen, desde su cuna, el lenguaje digital estuvo influido por la
dialéctica del fundador de la filosofía clásica alemana. Limitar la
interpretación de esta realidad a la superficialidad del empirismo positivista
es vaciarla de su contenido. Pero, en definitiva, nada escapa a la dialéctica,
ni siquiera la propia lógica formal.
Aunque el
sistema binario puede ser difícil de asimilar para una persona acostumbrada al
sistema decimal, para una computadora ese sistema es ideal porque corresponde a
la presencia o no de voltaje, al encendido o apagado de la corriente eléctrica,
o al verdadero o falso de un razonamiento simple. De esta forma, el código
binario disminuye los circuitos y la energía necesarios. Con este código no
sólo se pueden representar números y hacer operaciones matemáticas como ya
había mostrado Leibniz, sino se puede representar cualquier letra por su lugar
en el alfabeto, cualquier sonido por su lugar en una escala, cualquier color o pixel
por su asociación a un número, razonamientos simples por su representación
lógica en circuitos de verdadero o falso, una serie de instrucciones a través
de algoritmos, y de hecho se puede reproducir virtualmente cualquier cosa.
De esta forma,
una de las simbologías más antiguas regresó en la forma de la tecnología más
moderna; un ejemplo sorprendente de lo que en dialéctica conocemos como
“negación de la negación”. Lo más sorprendente es que a la realidad virtual
subyace la simple dualidad de unos y ceros, de la presencia y el vacío, del ser
y la nada. Pero la virtualidad es siempre una simplificación formal de la
realidad material infinitamente más compleja en contradicciones. En la realidad
material –como síntesis de múltiples determinaciones– las contradicciones son
mucho más profundas, intrincadas, enredadas y por sucesivos niveles de
complejidad.
Sólo por
mencionar algunos ejemplos: a nivel subatómico tenemos la dualidad de fuerza
nuclear débil y fuerte; a nivel atómico la dualidad de protones y electrones,
lo positivo y lo negativo; a nivel molecular las fuerzas electromagnéticas que
mantienen una gota de rocío pendiendo de una hoja tras la lluvia; a nivel
biológico la tensión entre vida y muerte, absorción y excreción; a nivel
psicológico tenemos lo consiente y lo inconsciente, lo instintivo y lo
racional; en la sociedad humana tenemos lucha de clases, contradicción entre
las condiciones objetivas y subjetivas y así sucesivamente sin fin.
Lo virtual sólo
es una sombra pálida de esa realidad material pero incluso esta sombra implica
la unidad de contrarios en la forma de unos y ceros. Heráclito, Hegel y Marx
deben estarse riendo en su tumba y Pitágoras regocijado de que toda la realidad
pueda reproducirse a través de números.
El
complejo de Terminator y la inteligencia artificial
“El apocalipsis
lo causará el capitalismo, no las máquinas” (Stephen Hawking).
Tanto Shannon
como Turing estuvieron involucrados en programas de ajedrez. Shannon publicó en
1949 un trabajo que describía un programa de ajedrez para computadora y Turing
desarrolló un algoritmo que podía jugar ajedrez pero que no pudo programar en
una computadora ya que los procesadores de su tiempo eran muy lentos. Turing
afirmó que si una computadora podía dar respuestas indistinguibles de las de un
ser humano esta máquina sería inteligente, en esto consiste el famoso “Test de
Turing”. Su interés en un programa de ajedrez iba en este sentido pues es un
juego ideal –con su espacio limitado, objetivo y reglas claros para cada pieza–
para probar sus test. En 1996 la computadora Deep blue logró ganar al campeón
mundial de ajedrez. Deep blue podía calcular 100 millones de jugadas por
segundo, pero Kasparov podía todavía ganarle a la máquina, de hecho pudo haber
ganado el match, pues la fuerza bruta de Deep Blue incluía cientos de miles de
jugadas inútiles. Actualmente cualquier programa de celular es capaz de ganarle
al campeón del mundo en ajedrez. Hasta este punto los programas de ajedrez eran
alimentados con conocimientos humanos, con un árbol de todos los grandes
maestros y campeones del mundo. La superioridad de dichos programas era el
resultado del compendio del conocimiento humano concentrado en la máquina
Pero en 2017 el
programa Alphazero, al que sólo se le habían programado las reglas del juego y
el objetivo de dar jaque mate, jugó millones de partidas contra sí mismo y en 4
horas el conocimiento adquirido, sin “prejuicios humanos”, ya superaba al
acumulado por la humanidad en toda la historia y a todos los programas de
ajedrez anteriores, llegando a un increíble elo de más de 3,400 puntos –el elo
más alto de un humano, obtenido por el actual campeón del mundo Magnus Carlsen,
es de 2,881 puntos–. Alphazero suele realizar jugadas que desafían la teoría de
aperturas y otros conceptos humanos, priorizando la actividad sobre otras
consideraciones estratégicas. Cuando Deep blue ganó el match a Kasparov la
prensa hizo comentarios sensacionalistas sobre el fin del ajedrez y la
supremacía de la inteligencia artificial sobre el intelecto humano. Pero de la misma
forma en que los automóviles no han hecho desaparecer al maratón, los programas
de ajedrez no han impedido que los humanos sigan jugando.
En realidad, la
concepción de inteligencia del test de Turing es bastante formal y tiene las
limitaciones propias del conductivismo, que sólo considera la respuesta
superficial de la conducta humana. Actualmente existen programas que son
capaces de responder preguntas, bots conversacionales e incluso existen
programas que pueden componer música, tal como había imaginado Ada Lovelace.
Pero es claro para cualquiera, aunque sea a un nivel intuitivo, que hay una
diferencia cualitativa entre las respuestas que da un programa como “Alexa”,
que conversar con una persona real, y también existe una diferencia entre lo
que produce un baterista real al sampleo de una máquina de ritmos. El carácter social y colectivo de la
existencia humana se expresa en la inteligencia y en todas las interacciones
sociales incluidas el lenguaje y la conversación. Esta complejidad explica la
psique humana compuesta en capas contradictorias muy profundas racionales e
irracionales, emocionales e intelectuales; dirigida por intereses personales,
sociales y de clase (en las sociedades divididas en clase). La inteligencia
artificial no tiene intereses ni pasiones y por ello sólo puede emular la
inteligencia humana de manera superficial, incluso aunque la supere por mucho
en capacidad de cálculo o en las operaciones por segundo que puede realizar.
Aunque ya es
una realidad que casi cualquier programa de ajedrez le gana al campeón del
mundo y no deja de fascinar una inteligencia artificial que aprende por sí
sola, no debemos perder el sentido de la proporción. La inteligencia artificial
es superior al humano sólo en un espacio limitado. Alphazero es incapaz de
aprender a jugar si de repente cambiaran las reglas del juego o las
características del tablero con las que fue programado. La diferencia
cualitativa de la inteligencia puede verse como un tema de desarrollo,
flexibilidad y contenido:
«Es fácil
conseguir que las computadoras muestren capacidades similares a las de un
humano adulto en pruebas de inteligencia, y difícil o imposible lograr que
posean las habilidades perceptivas y motrices de un bebé de un año»[7]. Sostuvo Miguel Lázaro, investigador de
inteligencia artificial.
El problema de
la inteligencia artificial es que es perfecta sólo en un estrecho sentido y su
determinismo la hace incapaz de adaptarse en un mundo cambiante e imperfecto
que el ser humano, también imperfecto, aborda de manera social y colectiva:
«Las decisiones
que tenemos que tomar a la hora de preparar un sándwich, manipulando y
ensamblando los ingredientes, parecen mucho más sencillas, pero sin embargo son
mucho más complicadas, desde la perspectiva computacional, que los juegos de
mesa en los que compite AlphaZero[8]».
Así que la
humanidad puede dormir tranquila ante el peligro de que un programa que sabe
jugar muy bien ajedrez, pero que no puede preparar un sándwich, tome el control
del mundo. Finalmente, la inteligencia artificial es sólo una herramienta de
los seres humanos, una forma de expandir la inteligencia humana de la misma
forma en que los libros expanden y conservan la memoria colectiva de la
humanidad. El peligro de que nos someta es tanto como el de que los libros de
la biblioteca de Alejandría derrocaran a los egipcios. Esa fantasía de The
Terminator, en donde las máquinas someten a la humanidad, es sólo producto del
sentimiento de alienación que surge de la producción capitalista, donde los
objetos del trabajo –convertidos en mercancías– dominan al productor y el
trabajador fabril se convierte en un apéndice de la máquina; en este sistema
las personas se cosifican como mercancías y las mercancías adquieren personalidad.
Pero esto es resultado de un orden social específico, no un efecto de las
máquinas ni de las computadoras por sí mismas.
La comparación
entre la inteligencia artificial y humana no puede haberse tomando esta última
en términos individuales o sólo considerando la superioridad de una computadora
sobre un campo determinado en relación con una persona aislada. La inteligencia
humana es un producto social, un cúmulo progresivo de conocimientos obtenidos
por la producción social y la experiencia colectiva de generaciones sucesivas.
Tomada en su conjunto la inteligencia humana es muy superior a la inteligencia
artificial. Cuando las barreras de clase que han dividido a la humanidad
durante milenios caigan esta inteligencia social cobrará un carácter mucho más
planificado y consciente; al caer el capitalismo y bajo una producción
planificada la inteligencia colectiva de la humanidad crecerá en cantidad y
calidad.
Actualmente la
inteligencia artificial se utiliza en toda clase de servicios como el bancario,
el llamado “internet de las cosas” y apps para los automovilistas, incluso el
sueño de Ada Lovelace de un programa componiendo música es ya una realidad.
Pero el desarrollo de todo el potencial de estas maravillosas tecnologías
depende de que toda la humanidad tenga acceso a las computadoras, móviles y al
internet. Esto es imposible mientras estos avances estén supeditados al lucro
privado que no invierte en donde no existe ganancia, aun cuando las personas en
países pobres necesiten teléfonos y computadoras.
Al mismo
tiempo, el desarrollo y aplicación de las llamadas “nuevas tecnologías” depende
en gran medida de que la humanidad tome control sobre sus propias relaciones
sociales. En una economía planificada sería posible y necesario aplicar todas
las tecnologías para garantizar la democracia de todos los trabajadores, el
intercambio y flujo de información. El trabajo se desarrollaría en un ambiente
verdaderamente colaborativo, comunal, que ahora sólo se produce en pequeños
espacios y en beneficios de las empresas privadas; las ideas e innovaciones se
intercambiarán sin el peso muerto de las patentes, y las conquistas en muchos
campos serán producto colectivo y en beneficio de todos. La interconexión
global en una economía planificada permitiría el desarrollo de programas e
inteligencias virtuales a un plano sin precedentes. Los niveles a los que
podría llegar esta tecnología son ya asunto de la ciencia ficción y de la
especulación audaz estilo Isaac Asimov.
[1] Engels,
Dialéctica de la naturaleza, México, Cartago, 1983, p. 94.
[2]Leibniz,
Gottfried; “Explicación de la aritmética binaria que únicamente utiliza
los
caracteres 0 y 1, junto a algunas notas sobre su utilidad y sobre cómo
ella le
da sentido a las antiguas figuras Chinas de Fu Xi”:
https://www.academia.edu/44176195/G_W_Leibniz_Explicaci%C3%B3n_de_la_aritm%C3%A9tica_binaria
[3] Carta de
Marx a Engels, 10 de mayo de 1870.
[4] Engels,
Dialéctica de la naturaleza, México, Grijalbo, 1983, p. 207.
[5] Ibid. 208.
[6] Ibidem.
[7]
https://elpais.com/elpais/2018/12/05/ciencia/1544007034_265553.html
[8] Ibid.
Fuente: marxismo.mx/